OpenCV实现二维码识别与定位

在家太闲，因此想找点事干，突然想起来我可以拍拍视频找机会挣个外快，于是我就思考了一下，找到了一个比较常见、简单但需要一定门槛的东西。

最终决定，那就做一个二维码扫描吧。

项目视频教程地址：https://www.bilibili.com/video/BV1La4y1t7bQ

开源地址：https://gitee.com/JogerQiao/joger_python_learning_code_record.git

1 效果展示

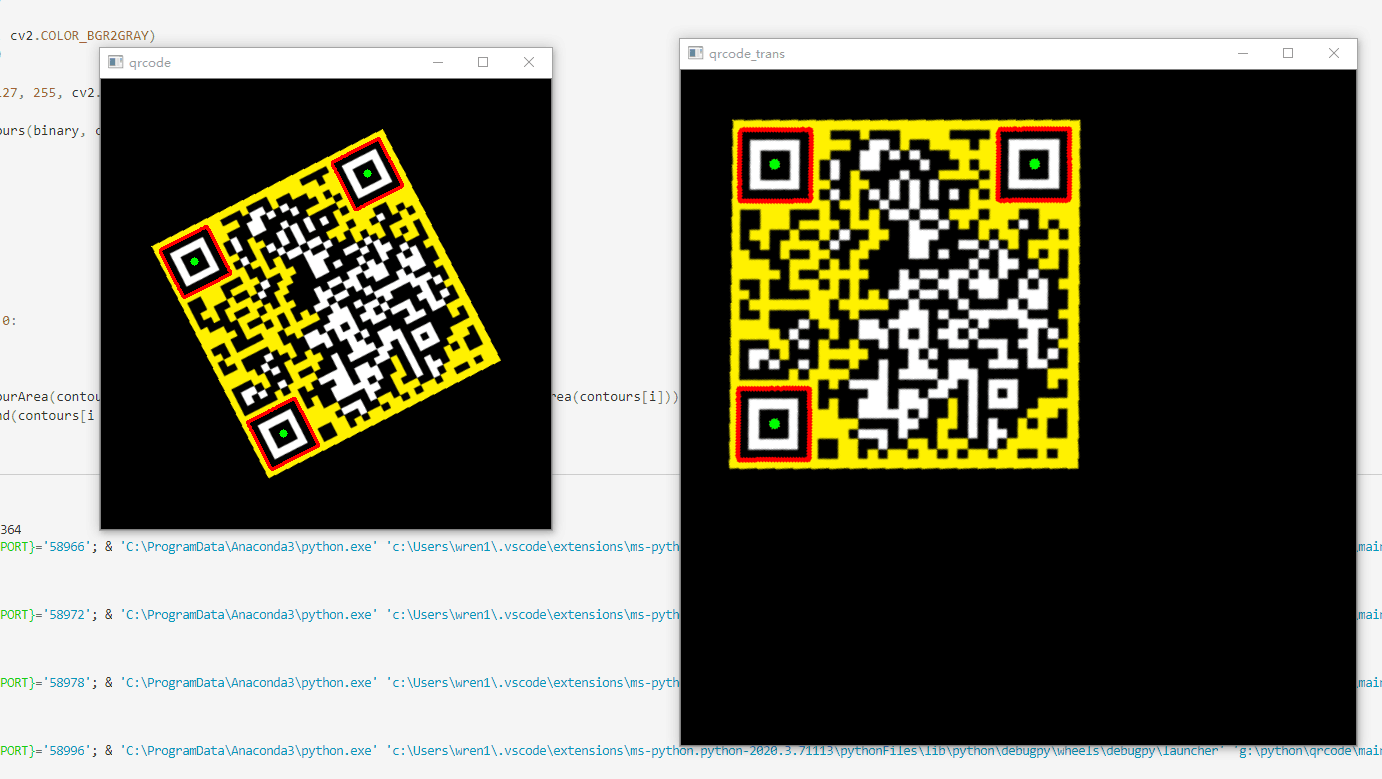
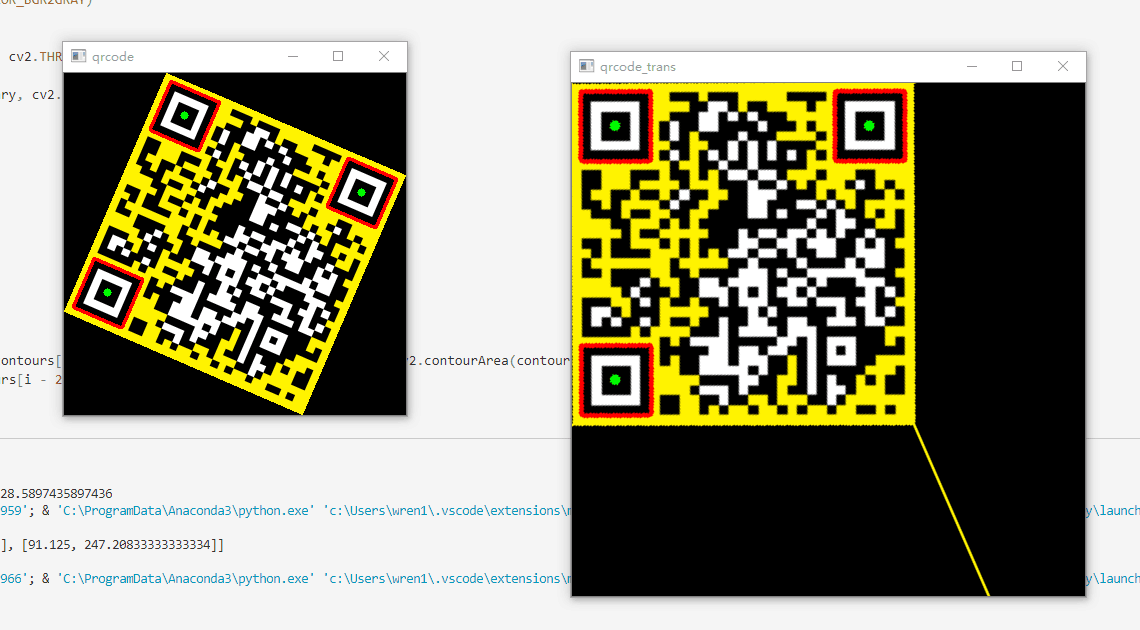
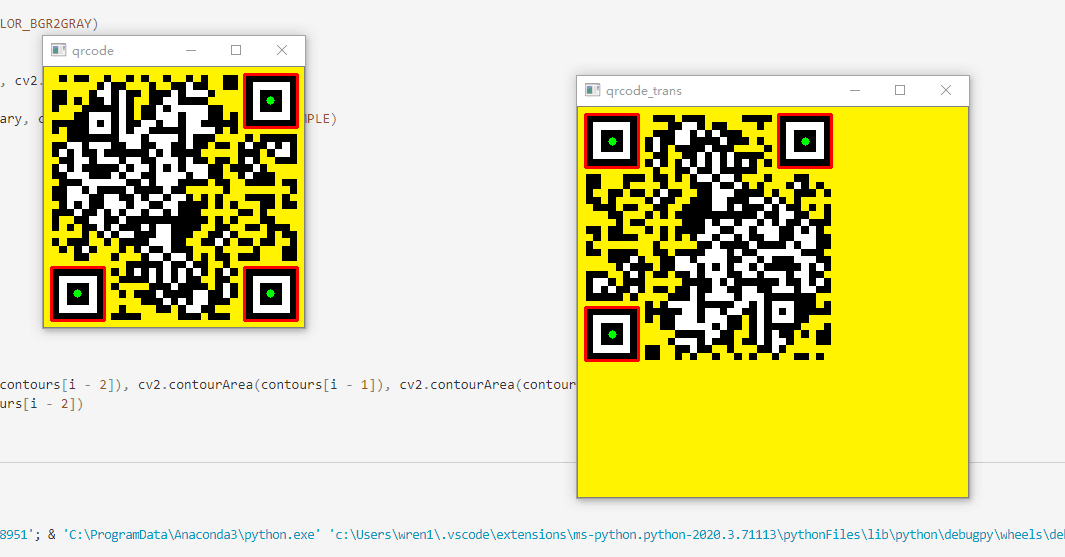
2 代码说明

整体代码思路是这样的：

• 通过三层轮廓找到三个以上的疑似定位点
• 使用面积比确定大概率疑似定位点
• 使用判断三个点是否组成直角三角形判断是否是疑似定位点
• 通过规律和右手定则计算三个点的顺序（直角点为1，之后顺时针依次）
• 使用仿射变换将二维码矫正到标准姿态，以便后期读取。

3 代码详解

本次使用的库包括：

import cv2
import numpy as np
import math

对图像文件进行打开、灰度和二值化处理并获取轮廓：

filename = 'qr.png'
print("file:",filename)
qrcode_input = cv2.imread(filename)
 
qrcode = cv2.cvtColor(qrcode_input, cv2.COLOR_BGR2GRAY)
# cv2.imshow("qrcode_gray", qrcode)
 
_, binary = cv2.threshold(qrcode, 127, 255, cv2.THRESH_BINARY)
contours = []
contours, hierarchy = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

对保存层级关系的轮廓hierarchy遍历，并找到有三级的且符合面积比为49:25:9关系的轮廓：

def isQR_Point(con1, con2, con3):
    # // 57.46
    base1 = con1 / 49
    base2 = con2 / 25
    base3 = con3 / 9
    base = min(base1, base2, base3)
    if (base1 - base <= base / 5 and base2 - base <= base / 5 and base3 - base <= base / 5):
        return True
    return False
 
level = 0
contours_sign = []
for i in range(len(hierarchy[0])):
    hie = hierarchy[0][i]
    if hie[2] != -1:
        # 说明有下一级
        level += 1
        pass
    elif hie[2] == -1 and level != 0:
        level += 1
        if level == 3:
            # 找到了很有可能是的
            if isQR_Point(cv2.contourArea(contours[i - 2]), cv2.contourArea(contours[i - 1]), cv2.contourArea(contours[i])):
                contours_sign.append(contours[i - 2])
                pass
            pass
        level = 0
    else:
        level = 0
        pass
    pass
 
cv2.drawContours(qrcode_input, contours_sign, -1, (0, 0, 255), 2)

在找到有可能是的轮廓中的中心点，并对这些点进行排序，满足

• 直角点为p1，之后顺时针依次为p2,p3的排列方式

'''
@name: 对点排序
@test: test font
@msg: 直角为p1，顺时针依次为p2,p3
@param {type} 
@return: 
'''
def sort_Point(points):
    p1, p2, p3 = points
    # 勾股定理 很难计算范围
    # 向量夹角
    v12 = [p2[0] - p1[0], p2[1] - p1[1]]  # 向量1->2
    v13 = [p3[0] - p1[0], p3[1] - p1[1]]
    '''
    @name: 计算两个向量夹角(数量积)
    @test: test font
    @msg: 使用公式cos_theta = (a * b) / (|a| * |b|) = (x1y1+x2y2)/(sqr(x1^2+y1^2) * sqr(x2^2+y2^2)) 欧几里德范数
    @param {type} 
    @return: 
    '''    
    def get_rad(v1, v2):
        # print((v1[0] * v2[0] + v1[1] * v2[1]) / (math.hypot(v1[0], v1[1]) * math.hypot(v2[0], v2[1])))
        return math.acos(
            (v1[0] * v2[0] + v1[1] * v2[1]) / (math.hypot(v1[0], v1[1]) * math.hypot(v2[0], v2[1]))
        ) / math.pi * 180.0
        pass
    
    # 判断三个角哪个是直角
    '''
    @name: 判断是否是这个范围内
    @test: test font
    @msg: 
    @param {type} 
    @return: 
    '''
    def r_in(value, target=90, miss=10):
        if value > target + miss or value < target - miss:
            return False
        return True
    # print(p1,p2,p3)
    # print(v12,v13)
    if r_in(get_rad(v12, v13), 90):
        # 如果p1为直角，那需要继续判断p2,p3
        if (v12[1] < 0 and v13[0] > 0) or (v12[0] < 0 and v13[1] < 0) or (v12[0] > 0 and v13[1] > 0) or (v12[1] > 0 and v13[0] < 0):
            # print(1)
            return [p1, p2, p3]
        elif (v12[0] > 0 and v13[1] < 0) or (v12[1] < 0 and v13[0] < 0) or (v12[1] > 0 and v13[0] > 0) or (v12[0] < 0 and v13[1] > 0):
            # print(2)
            return [p1, p3, p2]
        pass
    elif r_in(get_rad(v12, v13), 45):
        # 如果p1为45锐角，那可以判断p2,p3
        if math.hypot(v12[0], v12[1]) < math.hypot(v13[0], v13[1]):
            # print(3)
            # 使用叉乘判断顺时针逆时针 右手定则
            # 逆时针为[p2,p1,p3]
            # 顺时针为[p2,p3,p1]
            if np.cross(np.array(v12 + [0]), np.array(v13 + [0]))[2] > 0:
                return [p2, p3, p1]
            else:
                return [p2, p1, p3]
            # print(np.cross(np.array(v12 + [0]), np.array(v13 + [0])))
            
        else:
            # print(4)
            # print(np.cross(np.array(v12 + [0]), np.array(v13 + [0])))
            if np.cross(np.array(v12 + [0]), np.array(v13 + [0]))[2] < 0:
                return [p3, p2, p1]
            else:
                return [p3, p1, p2]
        pass
    return False
 
# 求定位点中心点坐标
sign_point_center = []
for contour in contours_sign:
    # 每个中心点都要确认
    # print(contour[:,0])
 
    tmpcont = contour[:,0]
    # print(tmpcont.shape)
    avg_x, avg_y = 0, 0
    for tmp_x, tmp_y in tmpcont:
        avg_x += tmp_x
        avg_y += tmp_y
        # print(tmp_x,tmp_y)
    avg_x /= contour.shape[0]
    avg_y /= contour.shape[0]
    # print(avg_x, avg_y)
    sign_point_center.append([avg_x,avg_y])
    cv2.circle(qrcode_input, (int(avg_x), int(avg_y)), 4, (0, 255, 0), -1)
    pass
 
# 对定位点排序，找到左上角1号点
# 分别为1号，2号，3号点
sign_point_center = sort_Point(sign_point_center)
print(sign_point_center)

之后求出仿射变换的目标点、变换矩阵并进行变换

# 对图形进行仿射变换
min_x, max_x = min([x[0] for x in sign_point_center]), max([x[0] for x in sign_point_center])
min_y, max_y = min([x[1] for x in sign_point_center]), max([x[1] for x in sign_point_center])
 
if max_x - min_x > max_y - min_y:
    # 取长边
    max_y = min_y + max_x - min_x
else:
    max_x=min_x+max_y-min_y
 
print(min_x, max_x, min_y, max_y)
 
# M = cv2.getPerspectiveTransform(
M = cv2.getAffineTransform(
    np.float32([
        [sign_point_center[0][0], sign_point_center[0][1]], [sign_point_center[1][0], sign_point_center[1][1]], [sign_point_center[2][0], sign_point_center[2][1]]
    ]),
    np.float32([
        [min_x,min_y],[max_x,min_y],[min_x,max_y]
        
    ])
)
 
# qrcode_output = cv2.warpPerspective(qrcode_input, M, (qrcode_input.shape[1] * 1, qrcode_input.shape[0] * 1), flags=cv2.INTER_LINEAR, borderMode=cv2.BORDER_REPLICATE)
qrcode_output = cv2.warpAffine(qrcode_input, M, (int(qrcode_input.shape[1] * 1.5), int(qrcode_input.shape[0] * 1.5)), flags=cv2.INTER_LINEAR, borderMode=cv2.BORDER_REPLICATE)
cv2.circle(qrcode_output, (int(min_x), int(min_y)), 8, (0, 255, 0), 1)
cv2.circle(qrcode_output, (int(max_x), int(min_y)), 8, (0, 255, 0), 1)
cv2.circle(qrcode_output, (int(min_x), int(max_y)), 8, (0, 255, 0), 1)
cv2.circle(qrcode_output, (int(max_x), int(max_y)), 8, (0, 255, 0), 1)